[PSAT Pick] 퀴즈 해결하면, PSAT 쉬워진다 (5)

[들어가며]

안녕하세요. 법률저널 <PSAT Pick>에서 상황판단 문제 중 퀴즈 유형의 문제에 관해 연재를 맡은 전명진 검수위원입니다. 많은 수험생들께서 어려워하시는 퀴즈 유형을 풀이하는 다양한 방법들과 그 출제 원리들을 소개 드리고자 합니다.

상황판단 퀴즈문제 (5)

[오늘의 문제]

이번 문제는 18년도 민경채에 출제된 작업능률 계산 문제입니다. 풀이가 간단한 만큼 조건 이해를 막힘없이 해내야 합니다. 작업능률문제는 뉴튼산의 형태로까지 이어질 수 있습니다.

키워드 : 작업능률, 뉴튼산, 수의 성질

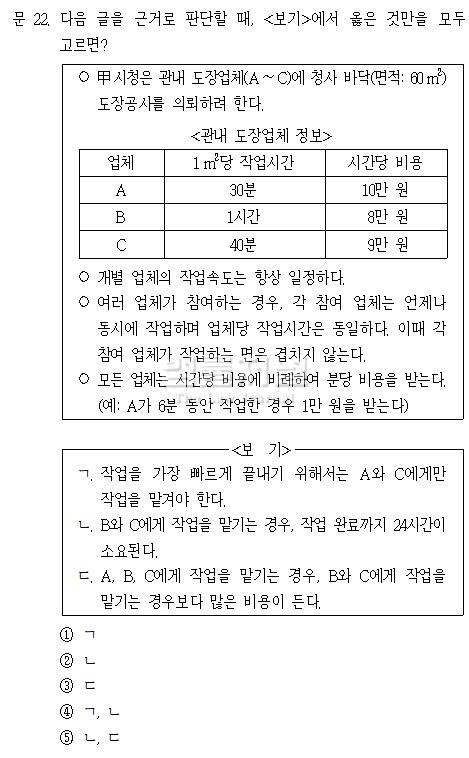
[풀이전략]

① ‘개별 업체의 작업속도가 일정하다는 조건’에 따라 1m²당 작업시간을 시간당(또는 분당) 작업량으로 변환할 수 있습니다.

② 총 업무 면적이 이미 주어져 있으므로 이를 이용하여 각 업체의 시간당 작업량을 전체에 대한 비율로 나타낼 수 있습니다. (이하 시간당 비율)

시간당 작업량전체 작업량

③ 시간당 비용을 분당 비용으로 미리 변환해 두는 것이 편합니다.

④ 각 업체의 시간당 비율을 합한 것의 역수는 총 작업 시간과 같습니다.

[문제해설]

① 각 개별 업체의 시간당 작업량은 다음과 같습니다.

▶ A: 2m²/h, B: 1m²/h, C: 1.5m²/h

② 이에 따라 각 업체의 시간당 생산량을 전체 작업량에 대한 비율로 나타낼 수 있습니다.

▶ 시간당 A: 전체 작업량의 1/30, B: 전체 작업량의 1/60, C: 전체 작업량의 1/40

▶ 분당 A: 전체 작업량의 1/1800, B: 전체 작업량의 1/3600, C: 전체 작업량의 1/2400

③ 각 업체의 분당 비용은 다음과 같습니다.

▶ 분당 A: 1/6만 원, B: 2/15만 원, C: 3/20만 원

④ ㄱ선지는 작업을 가장 빠르게 끝내기 위한 방법을 묻고 있습니다. 당연하지만 현재 조건에서는 A, B, C 업체 각각에 맡기는 경우보다는 두 개 이상의 업체에 맡기는 것이 더 효율적일 것입니다. 동시에 작업하는 업체 수의 한계를 정하지 않았으므로 세 개 모두 함께 일할 수 있습니다. 따라서 ㄱ은 틀린 선지입니다.

▶ A와 C가 함께 동시에 작업하는 경우: 1/{1/30+1/60}=20시간

▶ A와 B, C가 모두 함께 작업하는 경우: 1/{1/30+1/60+1/40}=40/3=13시간 20분

⑤ ㄴ선지는 위와 동일한 방법으로 구할 수 있습니다. 아래에 따르면 참입니다.

▶ B와 C가 함께 동시에 작업하는 경우: 1/{1/40+1/60}=24시간

⑥ ㄷ선지는 앞선 선지들에서 활용된 개념을 통해 각 경우 별로 업체들의 작업시간을 구하고 3을 이용하여 작업비용도 구할 수 있습니다. A와 B, C가 모두 함께 작업하는 경우 각각 13시간 20분씩 작업합니다. 즉, 800분씩 작업을 진행하므로 800 * (1/6+2/15+3/20) = 800 * 27/60 = 360만 원의 비용이 듭니다. 동일한 방법으로 B와 C가 함께 작업하는 경우를 구하면, 각각 1440분씩 작업을 진행하므로 1440 * (2/15+3/20) = 1440 * 17/60 = 408만 원의 비용이 드는 것을 알 수 있습니다. 따라서 ㄷ선지는 틀린 선지입니다.

[PSAT형 사고]

① 작업능률 문제는 단위변환 능력을 묻는 문제로도 생각할 수 있습니다. 시간당 작업량, 시간당 작업량과 전체 작업량 사이의 비율을 적극적으로 활용하여야 합니다.

② 협업 시 패널티 등을 주어 계산을 복잡하게 하거나, 본 문제처럼 작업능률과 분당 비용 구성이 서로 다른 경우 이르 적극적으로 활용하여 문제의 난이도를 높일 수 있습니다.

③ 간단한 작업능률 문제는 이번 문제와 같이 목표량이 고정값으로 주어지지만, 시간에 따라 변화하는 목표량을 가지는 경우도 있습니다. 목장의 소 문제가 가장 대표적인 유형인데, 초기값과 단위 시간당 유입량, 누출량을 활용하여 해결합니다. 이러한 경우의 문제 풀이를 뉴튼산이라고 합니다. 뉴튼산은 다음과 같은 구조로 이루어 집니다.

작업대상 1단위 당 초기값 X
작업대상 1단위 당 시간 1단위에 추가(유입)되는 작업량 Y
행위주체 1단위 당 시간 1단위에 해결(누출)하는 작업량 Z

1, 2, 3과 작업대상 n단위, 행위주체 m단위를 통해 식을 만들면 nX+nYt-mtZ=??의 꼴이 됩니다. 이와 같은 식을 두 개 이상 주고 이를 연립하여 Y와 Z 사이의 관계를 구하는 것이 뉴튼산 문제의 풀이법입니다.

[마치며]

PSAT든 LEET든 각종 적성검사에 활용되는 대부분의 퀴즈들은 이미 수 없이 재활용되어 온 것들 입니다. 대표적인 퀴즈의 명칭만 알면 혼자서도 쉽게 찾아 보고 익힐 수 있으니 포기하지 말고 유형의 범위와 깊이를 넓혀가셨으면 합니다. 질문이나 건의가 있으신 경우 댓글과 이메일(psatpick@gmail.com) 남겨주시면 피드백드릴 수 있도록 하겠습니다.

전명진 다른기사 보기

xxx