[들어가며]

안녕하세요. 법률저널 <PSAT Pick>에서 상황판단 문제 중 퀴즈 유형의 문제에 관해 연재를 맡은 전명진 검수위원입니다. 많은 수험생들께서 어려워하시는 퀴즈 유형을 풀이하는 다양한 방법들과 그 출제 원리들을 소개 드리고자 합니다.

“처음 3번의 기고 이후, 방향성에 대한 고민으로 한 주 쉬어가는 과정을 거쳤습니다. 1차 시험 일정이 예년보다 빨라지면서 더 이상 고민을 할 시간이 없어 일단 기존과 같은 포맷으로 진행하는 것으로 결정하였습니다. 대신 시험장에 들어가시기 전에 보실 수 있도록 퀴즈정리 자료집도 만들고 있으니 기대해주세요.”
 

[오늘의 문제]

이번 문제는 18년도 5급 공채(가 책형)에 출제된 리그전 승패계산 문제입니다. 여러 조건들이 상정된 리그전에서 경우의 수를 구하는 문제입니다.

키워드 : 토너먼트, 리그, 승패표, 승점계산, 경우의 수
 

[풀이전략]

1 리그전에서는 총 경기 수와 경기 횟수를 근거로 잔여경기를 파악할 수 있습니다. 잔여경기에 따른 경우의 수를 구할 수 있어야 합니다.

2 첫 번째, 두 번째 조건을 합하여 2018년 순위에 따른 선수 선발 순위를 정리해두어야 합니다.

3 무승부가 없고, 시즌 종료시 최종 등수가 같은 경우는 나오지 않는다는 조건을 놓치면 안됩니다.

[문제해설]

1 첫 번째와 두 번째 조건을 정리하면 다음과 같습니다.

1Round				2Round
1	2	3	4	1(5)	2(6)	3(7)	4(8)
3, 4등*		2등	1등	1등	2등	3, 4등
* 2018년 등수를 의미함

2 승수가 많을수록 등수가 높다는 점을 고려하면, 甲은 50승을 하였으므로 어떠한 경우에도 최종순위가 1등이 됩니다. (乙, 丙, 丁이 잔여 경기에서 전승을 하는 경우에도 甲의 승수에는 미치지 못합니다.) 따라서 甲은 반드시 4순위, 5순위(2R 1순위)로 선수를 선발하게 됩니다. 따라서 ㄱ. 은 올바른 선지입니다.

3 마찬가지로 丁은 반드시 최종 4등입니다. 조건에 따르면 최종순위 3, 4등이 1라운드 1, 2순위 추첨에 참여하므로, 丁은 1라운드 1순위 선발 추첨에 반드시 참여합니다. 따라서 ㄹ. 은 틀린 선지입니다.

4 乙은 잔여경기가 1경기 남아 있습니다. 乙이 나머지 경기에서 승리할 경우 丙은 반드시 3위가 됩니다. 다음은 乙의 잔여경기 승패에 따라 가능한 경우의 수를 정리한 것입니다. 승패 동률이 나올 수 없다는 조건을 기억하고 있다면 간단히 작성할 수 있을 것입니다.

위 표에서 乙과 丙의 등수가 확정되지 않는 것을 확인할 수 있으며, 예외 상황의 승패 조건 또한 확인할 수 있습니다. 좀 더 높은 난이도 문제였다면 활용될 수 있는 조건입니다.

5 乙이 2등을 한 경우에는 丙이 3등이므로, 4등인 丁과 1, 2순위 선발권을 무작위로 나눠 가지게 됩니다. 따라서 丙이 1순위 선발을 하게 되는지, 2순위 선발을 하게 되는지에 따라 다른 선발 결과가 나올 것 이라고 추측할 수 있습니다. 각 경우의 선발 결과는 다음과 같이 적어보는 것이 좋습니다.
 

丙이 1순위인 경우 丙이 H를 선발하므로 乙은 H를 선발할 수 없습니다. 또한 丁이 1순위인 경우에도 丙의 선택 순위가 乙보다 먼저이므로, 乙은 H를 선발할 수 없습니다. 따라서 ㄴ. 은 틀린 선지입니다.

위와 같이 표로 만들지 않더라도 丙이 乙보다 먼저 선발하게 되면 乙이 H를 선발하지 못함은 명백합니다.

6 丙이 2등을 한 경우에는 乙이 3등이므로, 乙이 반드시 丙보다 먼저 선발을 하게 됩니다. 이와 추첨을 고려하여 가능한 경우의 수를 나타내면 다음과 같습니다.
 

乙과 丁이 丙이 선호하는 A와 H를 먼저 선발할 것이므로 丙은 1R에서 C를 선발할 수 밖에 없습니다. D 또한 4, 5순위로 선수를 선발하는 甲이 먼저 선발하게 되어 丙은 F를 선발할 수 밖에 없습니다. 따라서 丙이 2등인 경우 丙은 C와 F를 반드시 선발합니다. 즉, ㄷ. 은 바른 선지입니다.

[PSAT형 사고]

1 잔여 경기에 따른 순위를 예측하여 문제를 해결하여야 합니다. 이 문제에서는 순위 예측의 범위를 선지에서 좁혀주어 문제의 난이도가 낮았습니다만, 16년도 5급 공채 4책형 32번 문항과 같이 승점을 바탕으로 문제를 해결하여야 하는 경우나, 11년도 민경채 인책형 22번 문항과 같이 잔여경기의 경우의 수를 모두 따져야 하는 경우 체감 난이도가 높아질 수 있습니다.

2 토너먼트 - 토너먼트는 일정한 대진에 의하여 승리한 사람(팀)만이 2·3·4회전으로 올라가, 마지막에 두 사람(팀)이 대전하여 우승을 겨루는 방식으로 승자전이라고도 합니다. 이때 N팀이 참여한 토너먼트의 전체 경기수는 N-1입니다. 상황판단에서 문제로 나올 경우 규칙에 따라 토너먼트를 배정하거나, 토너먼트의 총 경기수를 예측하는 형태의 문제로 출제될 수 있습니다.

3 리그 - 리그(풀 리그)는 N개의 팀이 참가하였을 때, 모든 팀이 서로 1번 이상은 경기를 치르는 것을 의미합니다. 이때 전체 경기수는 _NC₂가 됩니다. 리그는 그 자체로는 매우 단조로운 구조를 띄고 있어 토너먼트와 혼합되거나 승패, 승점을 판단하는 문제로 출제됩니다.

[마치며]

PSAT든 LEET든 각종 적성검사에 활용되는 대부분의 퀴즈들은 이미 수 없이 재활용되어 온 것들 입니다. 대표적인 퀴즈의 명칭만 알면 혼자서도 쉽게 찾아 보고 익힐 수 있으니 포기하지 말고 유형의 범위와 깊이를 넓혀가셨으면 합니다. 질문이나 건의가 있으신 경우 댓글과 이메일(psatpick@gmail.com) 남겨주시면 피드백드릴 수 있도록 하겠습니다.

[오늘의 보너스 문제]

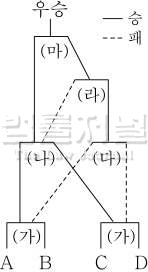
Q.. 4개의 야구팀 A, B, C, D가 다음과 같은 방법으로 우승팀을 결정하기로 하였다.   (가) A팀과 B팀이 경기를 하고, C팀과 D팀이 경기를 한다. (나) (가)에서 이긴 팀끼리 경기를 한다. (다) (가)에서 진 팀끼리 경기를 한다. (라) (나)에서 진 팀과 (다)에서 이긴 팀이 경기를 한다. (마) (나)에서 이긴 팀과 (라)에서 이긴 팀이 경기를 한다. (바) (마)에서 이긴 팀이 우승팀이 된다. 매 경기에서 각 팀이 이길 확률은 모두 절반으로 같다고 하자. A팀이 우승했을 때, A팀이 (가)에서 이겼을 확률은 q/p이다. 이때, p+q의 값을 구하시오. (단, p와 q는 서로소인 두 자연수이다.)

 

[해설]

이 문제는 더블 엘리미네이션 토너먼트에 대해 이해하고 조건부확률을 활용하여 해결하여야 합니다. 더블 엘리미네이션 토너먼트는 2회 패할 때까지 대진표에서 이탈되지 않는, 대진표 작성의 운을 배제하는 형태의 경기방식입니다. A가 우승한 경우에 (가)에서 승리했을 확률을 구하는 것이므로, A가 우승하는 모든 경우의 수를 구하고, 이때 (가)에서 승리한 비율을 구하면 됩니다.

A가 우승하는 모든 경우는 다음과 같습니다.
 

(가)에서 승리한 경우	(가) 승 (나) 승 (마) 승	확률 : 1/8
	(가) 승 (나) 패 (라) 승 (마) 승	확률 : 1/16
(가)에서 패배한 경우	(가) 패 (다) 승 (라) 승 (마) 승	확률 : 1/16

위 표에 따르면 A는 1/4의 확률로 우승을 할 수 있습니다. 이때 (가)에서 승리한 경우의 확률이 3/16이므로 A가 이미 승리한 경우를 분모로 하여 조건부확률을 계산하면 3/4입니다. 따라서 p+q는 7입니다.

“이 문제는 2009년 서울특별시 주관 학력평가 고3 가형 확률과 통계 23번 문제입니다. 2010년 5급 공채 선 책형 16번에 나온 문제와 거의 동일하여, 오늘의 보너스 문제로 선정하였습니다.”